- > Home
- > Services
- > Math as Art
As the study of natural and abstract patterns and patterning, mathematics is an inherently creative and artistic pursuit.
Unfortunately, many students have been mistaught that math is a dry, rote, one-dimensional activity devoid of originality or inventiveness and lacking any real connection to the arts.
Fortunately for me, I was not one of them.
On the contrary, I've always been enthralled by the astonishing musicality of mathematics and entranced by its subtle aesthetics, alluring forms, and fascinating puzzles to be solved.
Advances in computing technology have made possible the widespread discovery and appreciation of the sublime beauty of mathematics. The art of math can now be enjoyed by all!
I hope you'll delight in the following graphs of mathematical relations I created involving nothing more sophisticated than high school precalculus.
Designed in 2018 using Google Search's graphing calculator:
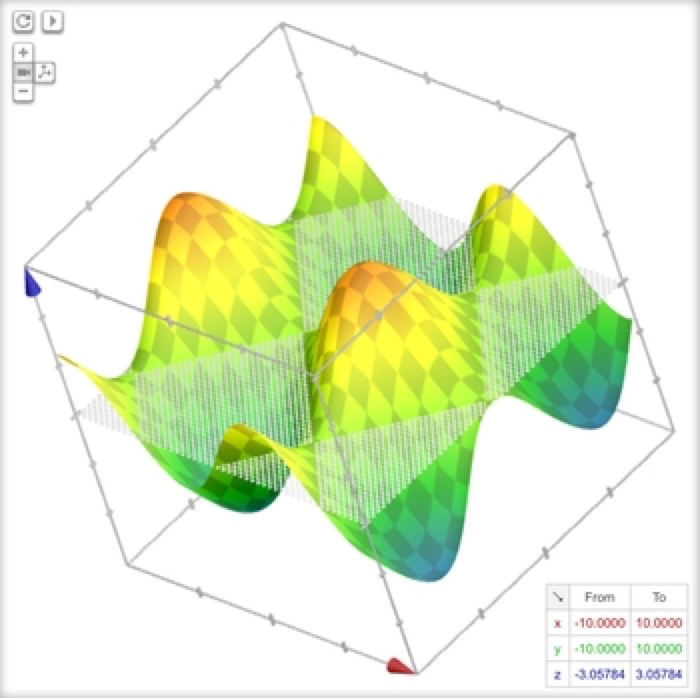
Egg Carton
z = sin(x/2)+cos(y/2)
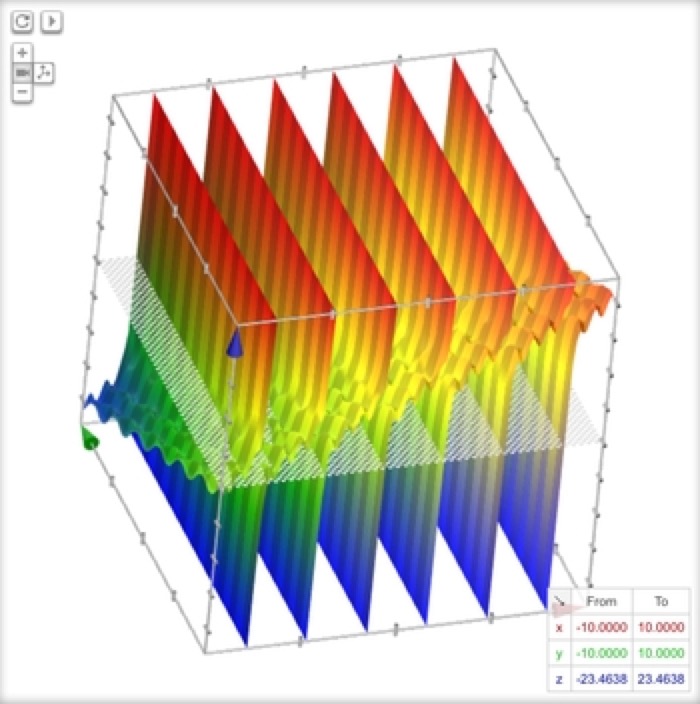
Wrinkled Paper
z = x-y+tan(x)-cos(8x-sin(2y))
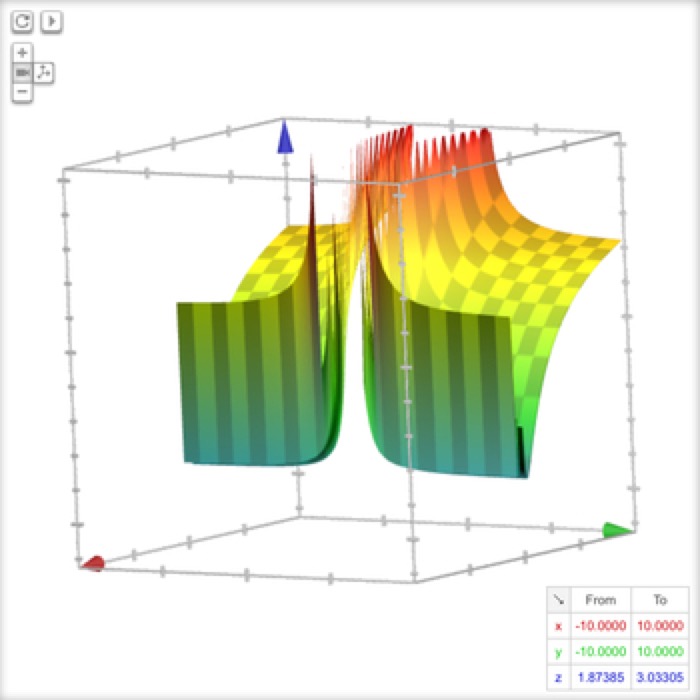
Fancy Lapels
z = arcsec(sin(1/x)-cos(1/y))
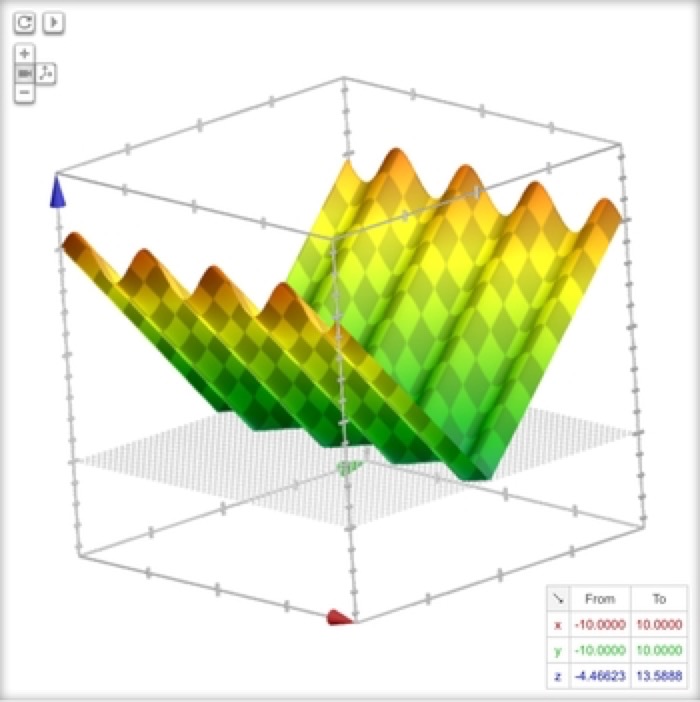
Corrugated V-Roof
z = abs(sin(2x)-y)
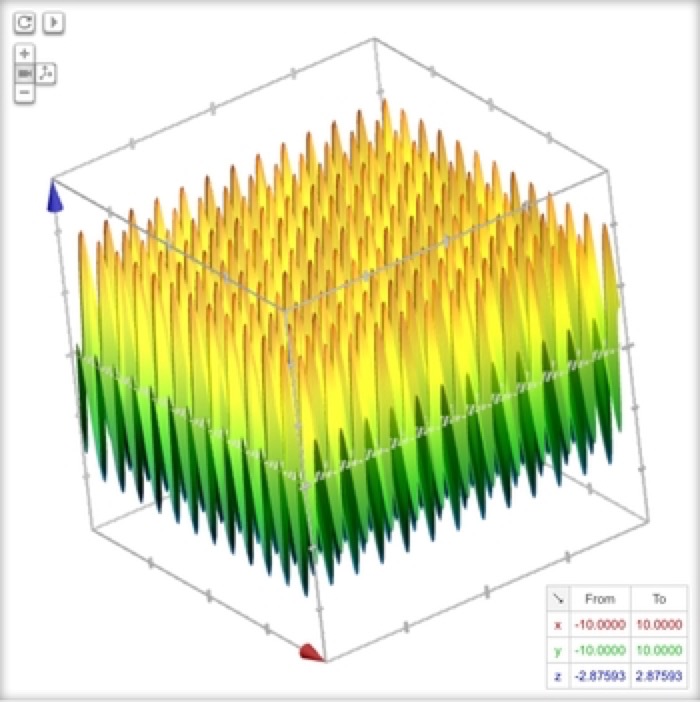
Bed o' Nails
z = sin(4y)+cos(4x)
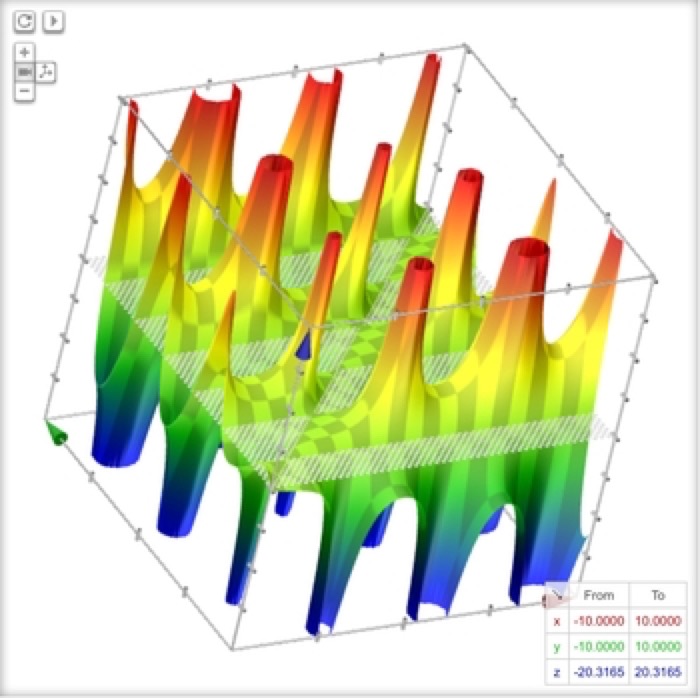
Arizona Desert
z = (x-y)/(sin(x)+1/cos(y))
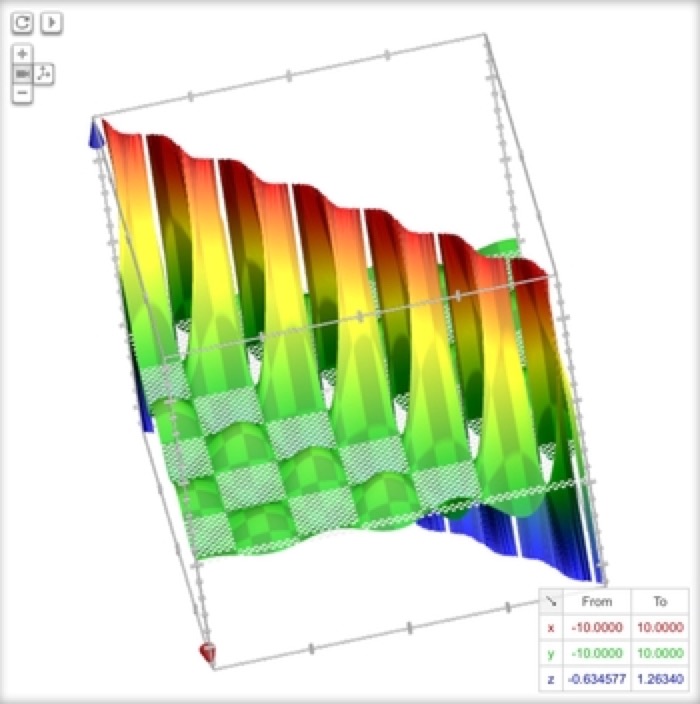
Celery Row
z = (sin(x)cos(y))/(x-y)
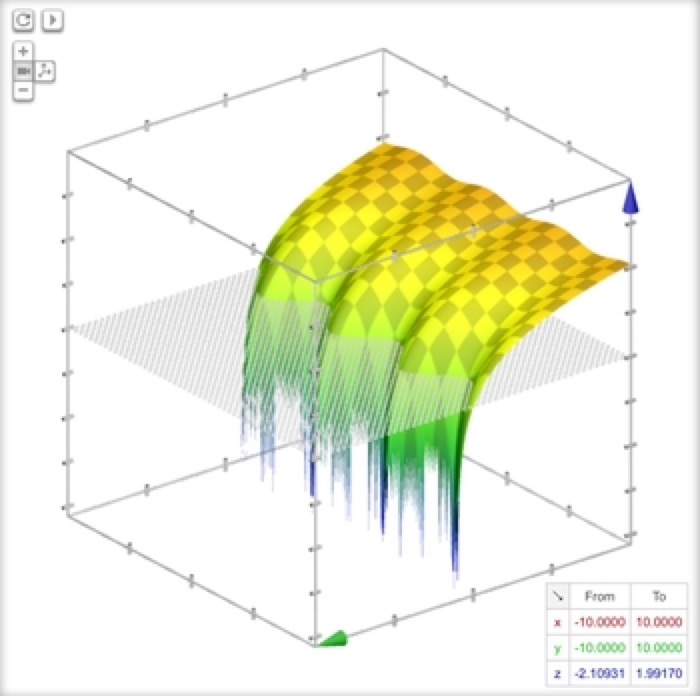
Three Fingers
z = log(sin(1.1x)-y)
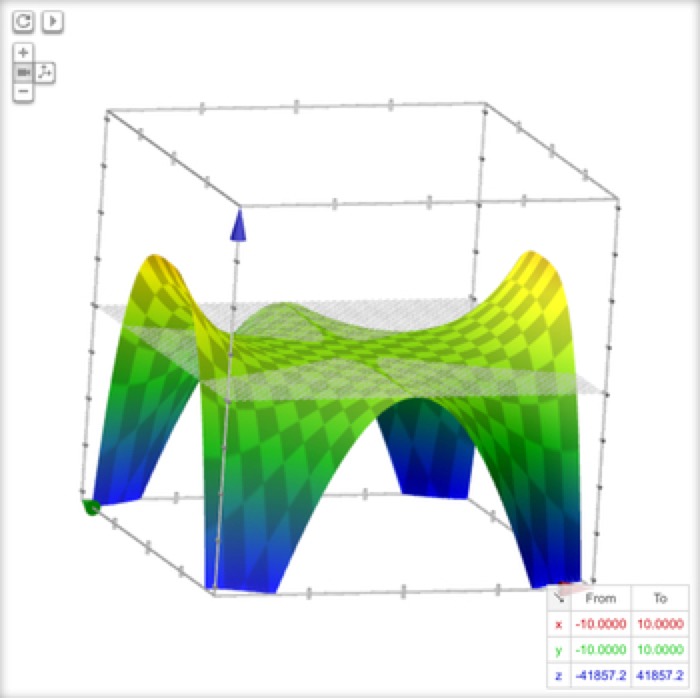
Plastic Chair
z = -abs(x)+2x^4-abs(x^2*y^3)
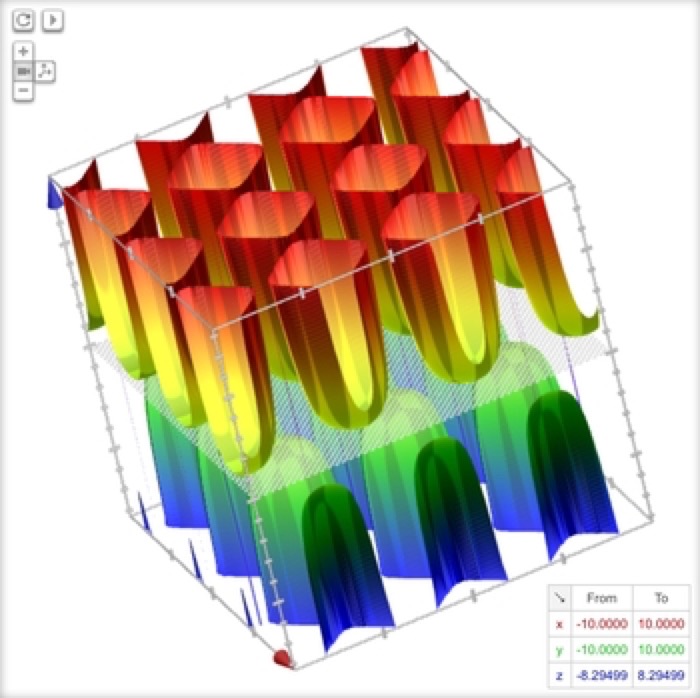
Lettuce Garden
z = 1/(sin(x)-cos(y))
Designed in 2018 using Wolfram Alpha:
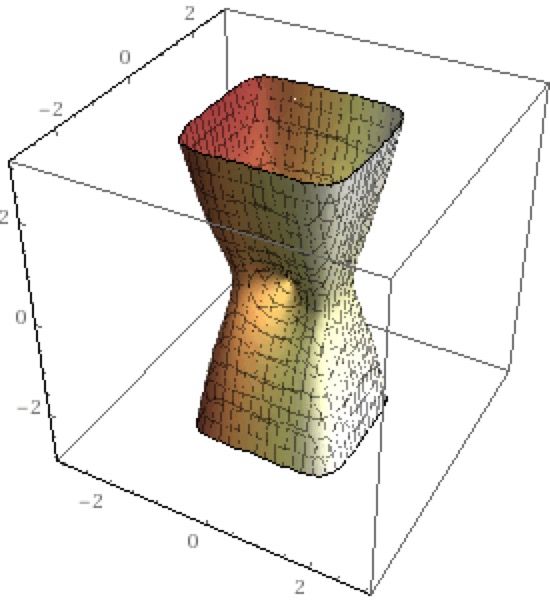
Dimpled Vase
z^2 = x^6-x^2+y^6+y^2
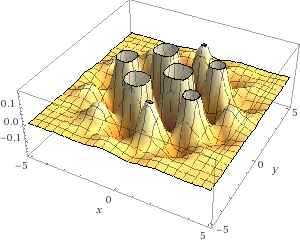
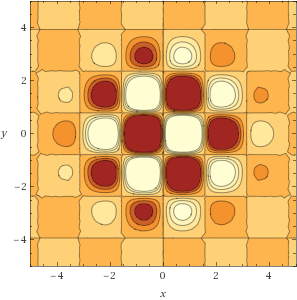
Mesa Group with Hills and Valleys
z = sin(2x)cos(2y)exp(-(x^2+y^2)/6)
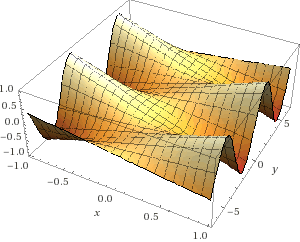
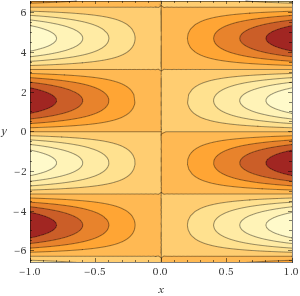
Slanting Waves
z = xsin(y)
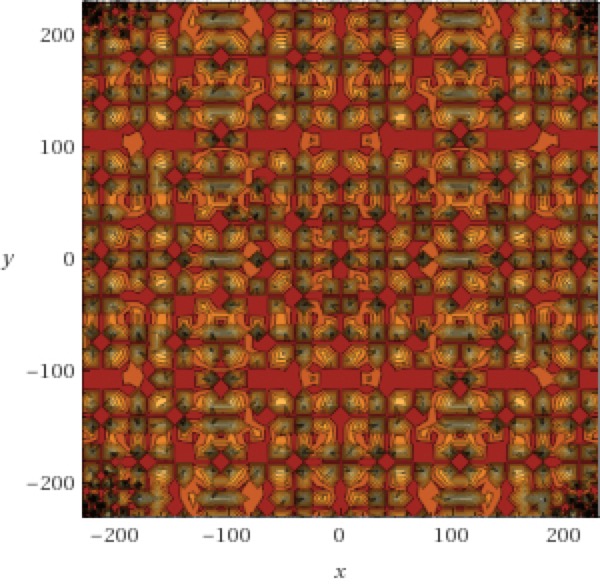
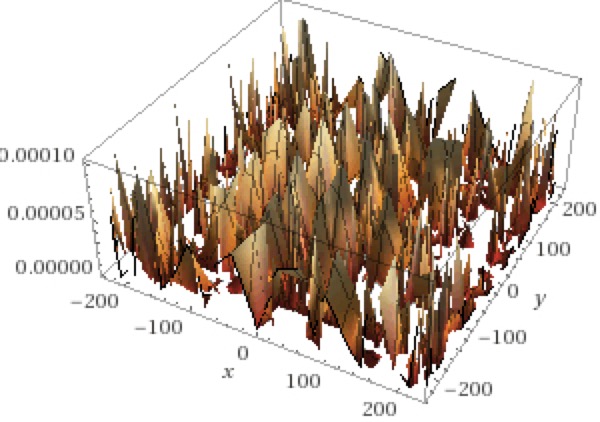
Tartan Forest
z = tan(.01sin(x)cos(y))^2
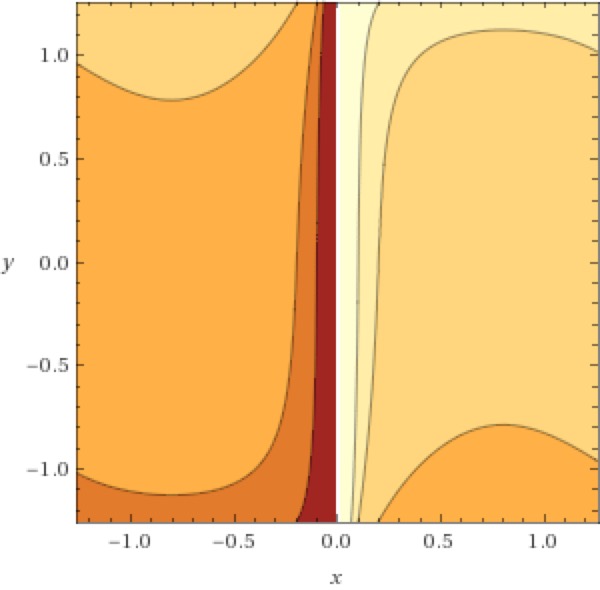
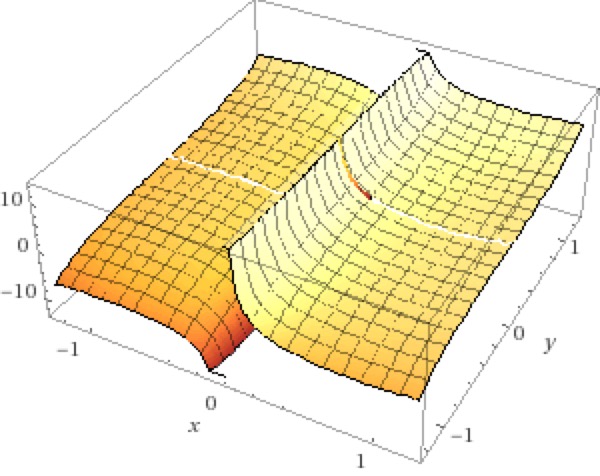
Techtonic Rift
z = x^3+tan(y)+cot(x)+y^3
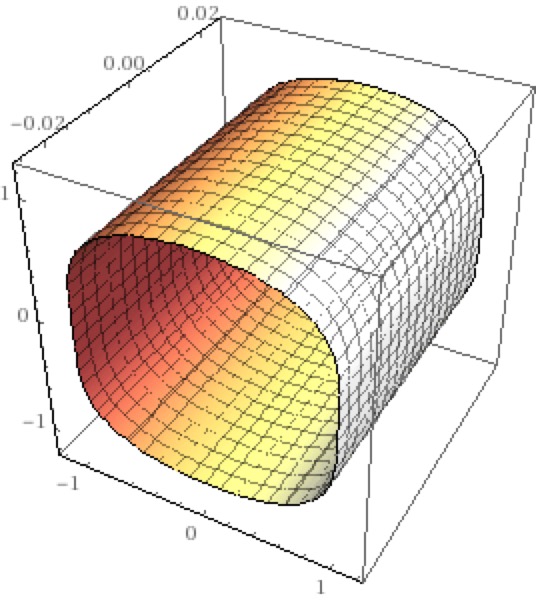
Squarish Tube
x^2-y^3+z^4 = 1
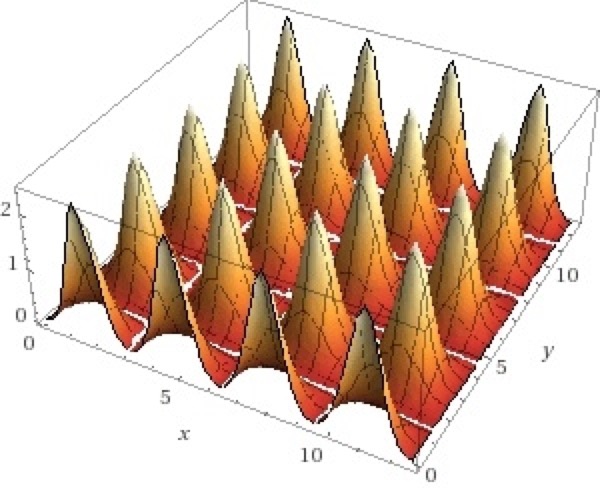
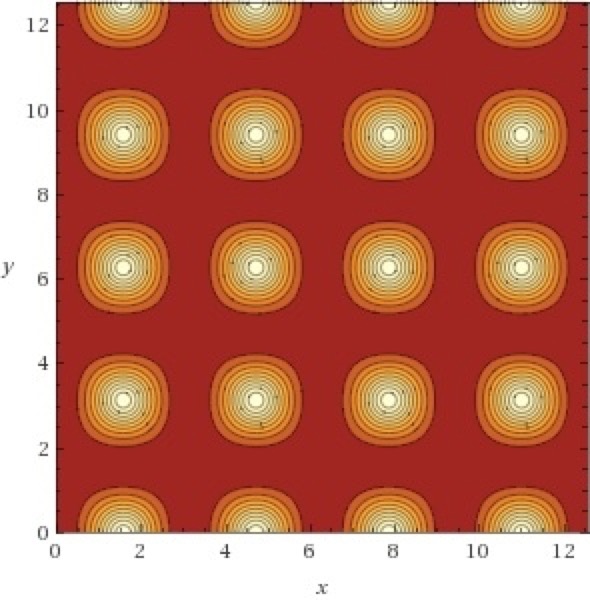
Spikes
z = tan(sin(x)cos(y))^2
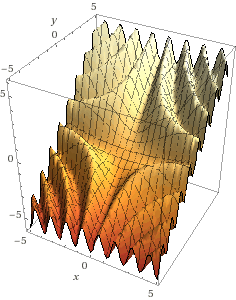
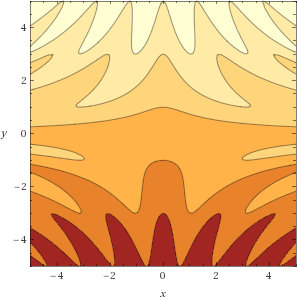
Wavy Incline
z = -cos(xy)+y
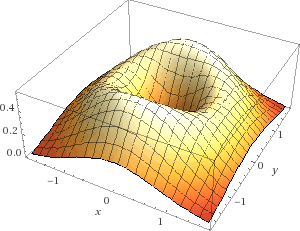
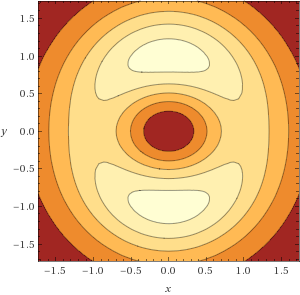
Gaping Maw
z = (x^2+1.5y^2)*e^(-x^2-y^2)
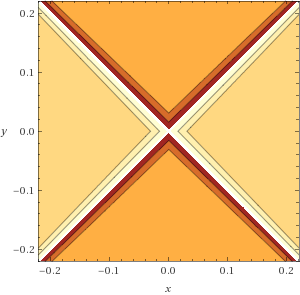
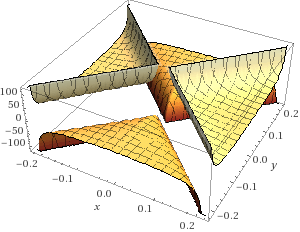
X Marks the Spot
z = (arccos(abs(x)+abs(y))/arcsin(abs(x)-abs(y))
Designed in 2018 using Apple's Grapher app:
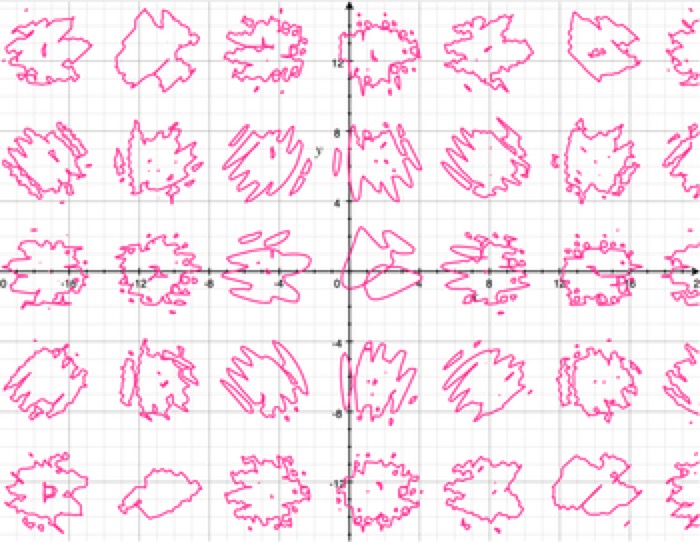
Splotches
sin(sin(x)+cos(y)) = cos(sin(xy)+cos(x))
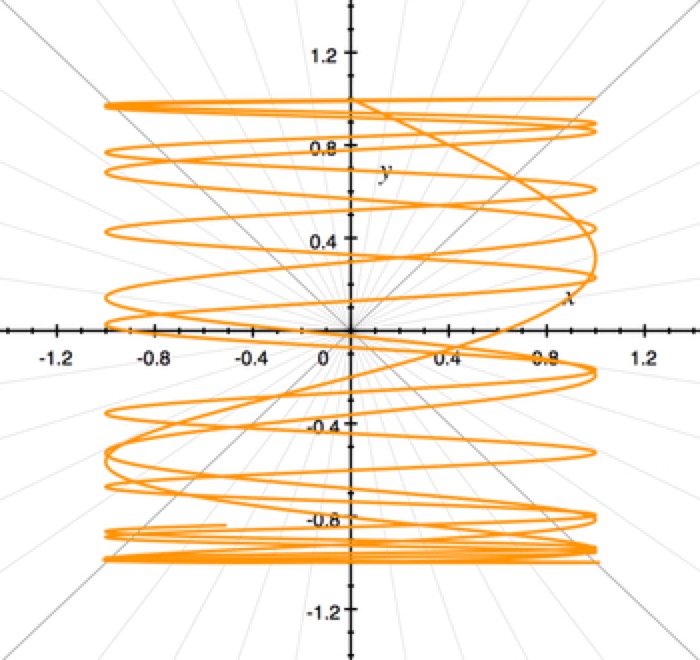
Slinky Toy
x = sin(t^2)
y = cos(t)
t = {0..10}
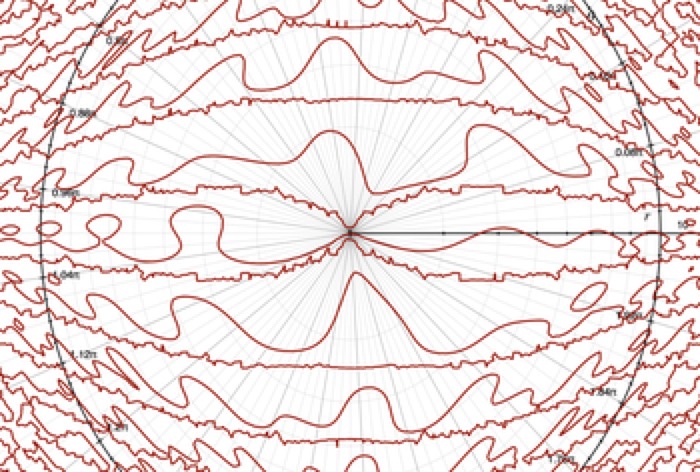
The Wiggles
cos(2x)-sin(xy)-tan(2y) = .5
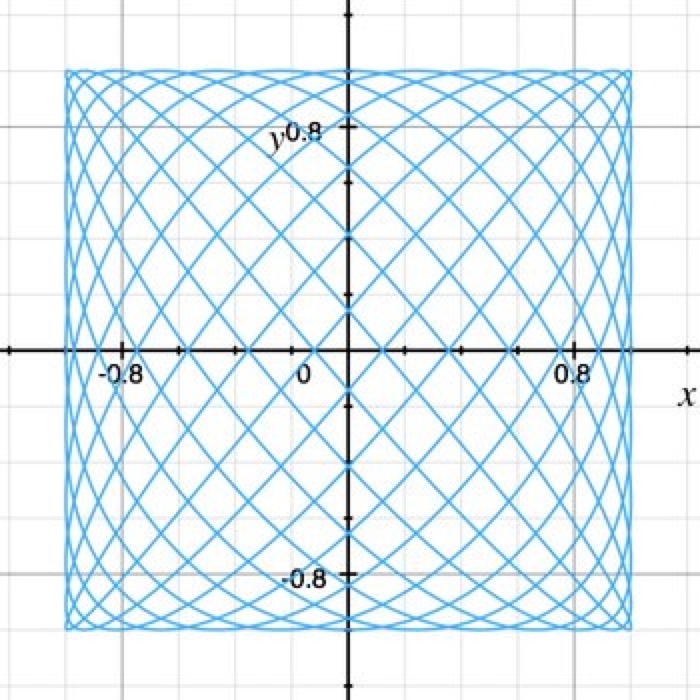
Basket Math
x = cos(11t)
y = sin(13t)
t = {0..2π}
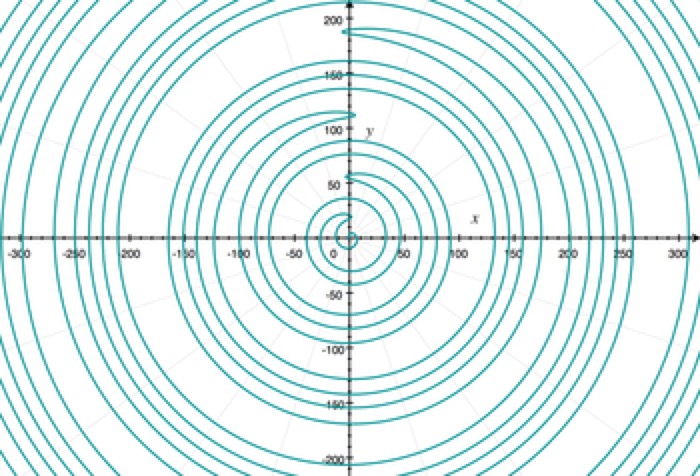
Double-Back
r = t^2-t
𝜃 = tsin(t)
t = {0..40}
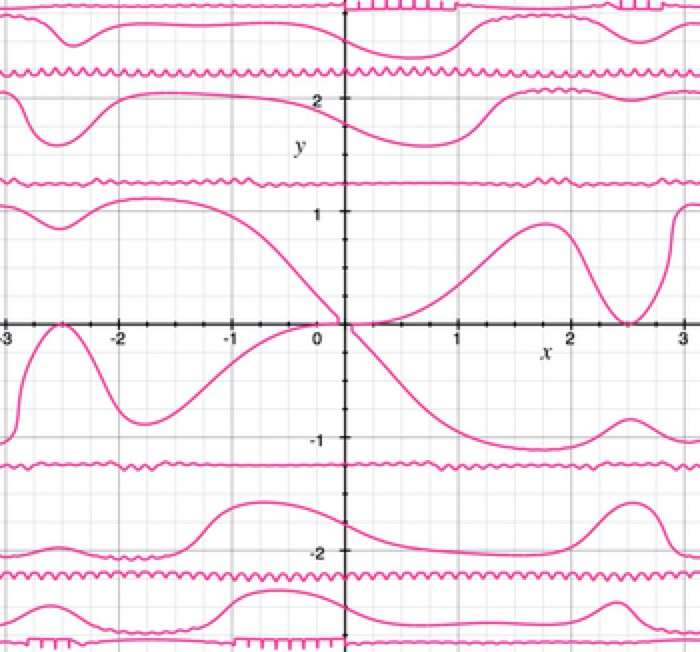
Line Dancing
cos(x^2)+sin(xy)+tan(y^2) = 1
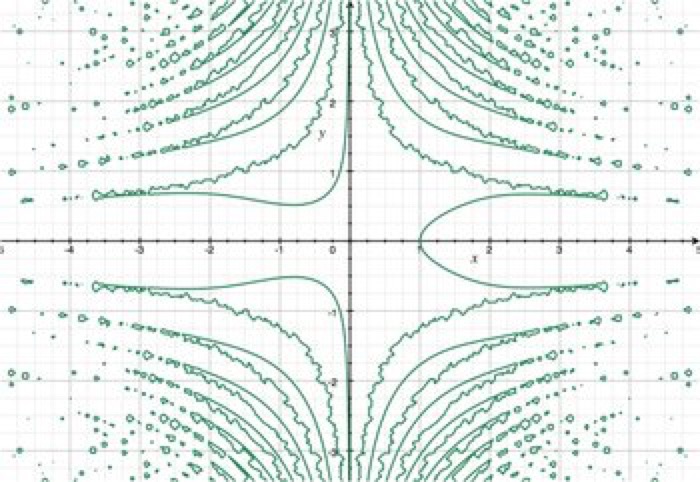
Controlled Chaos
x^3 = 1+7tan(xy^2)
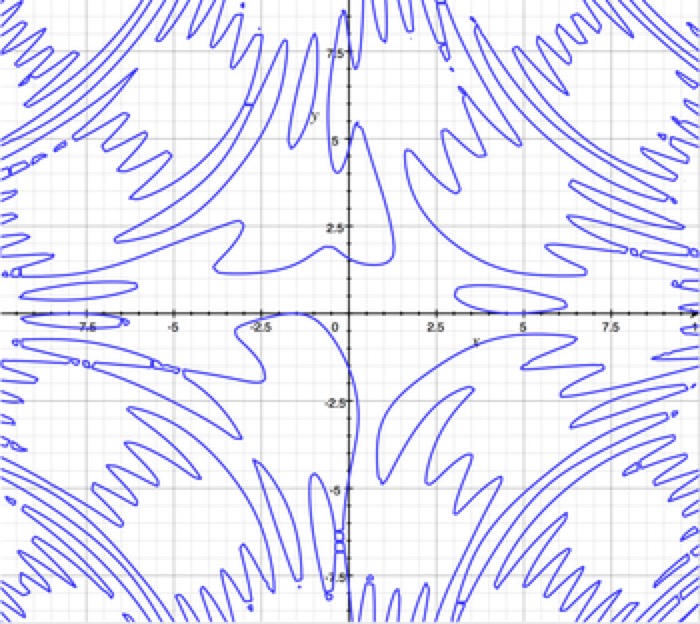
Ripples
sin(xy) = cos(y)+sin(x)
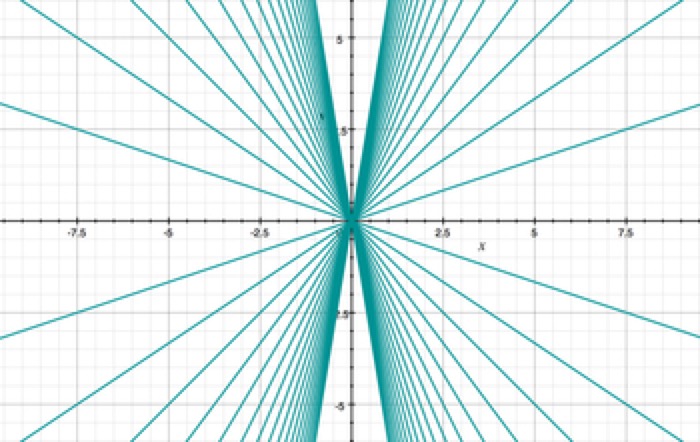
Convergence
y = kx/3
k = {1..18}
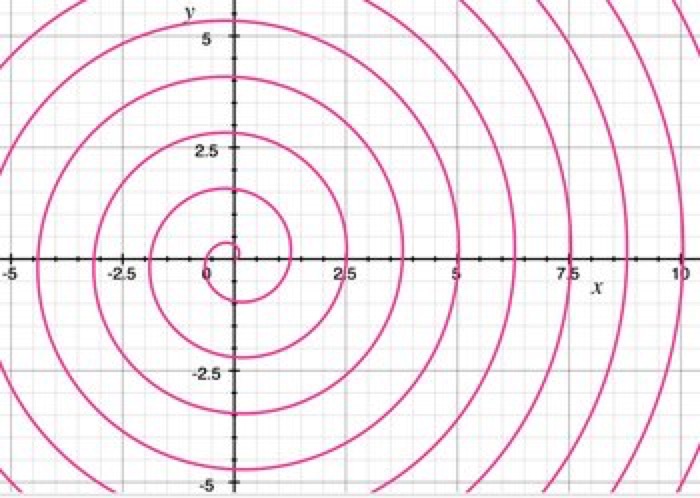
Spiral
x = (u/5)cos(u)
y = (u/5)sin(u)
u = {0..20}

Fender Butterfly
r = sec(x)
y = tan(x)+cot(x)+K
k = {-5..5}
Designed in the late 1990's using the pioneering Mac app Graphing Calculator, later NuCalc:

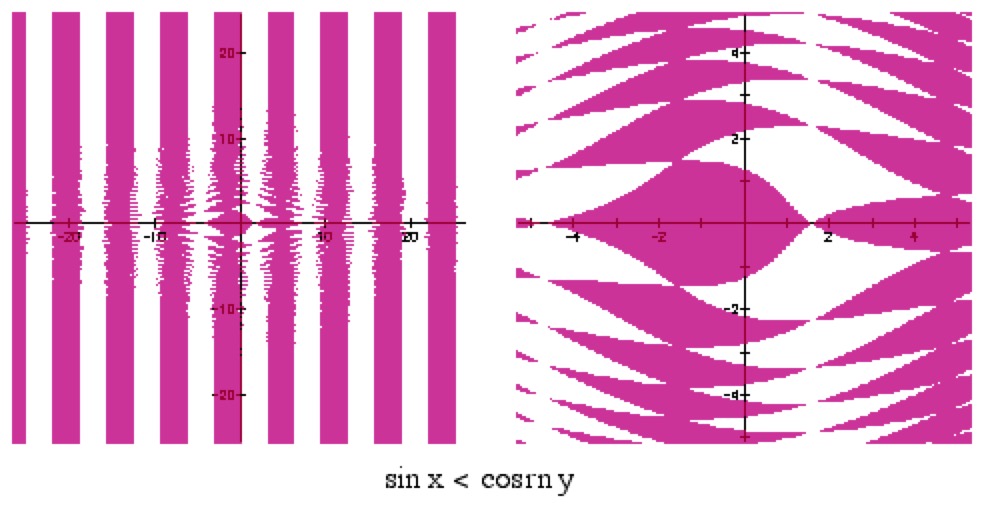

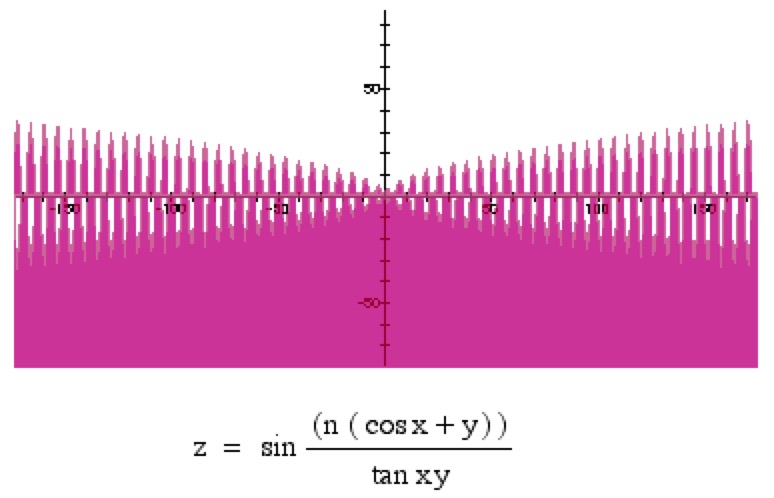
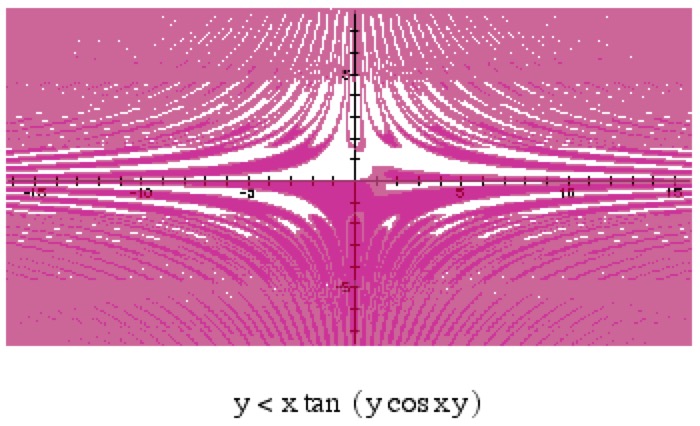
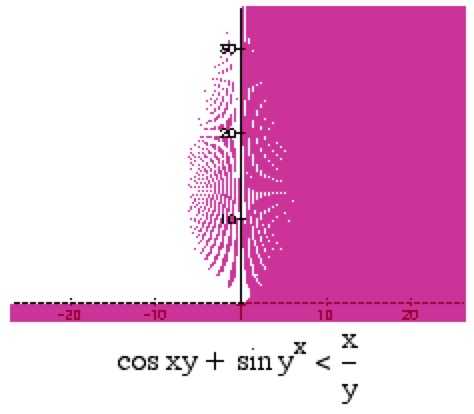
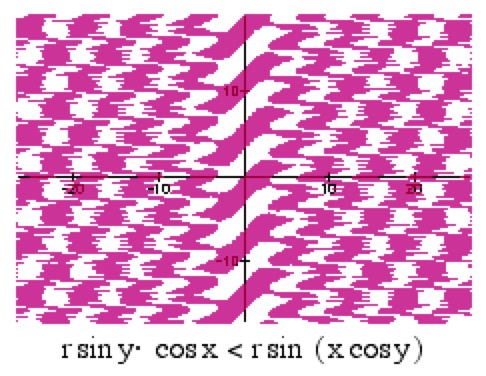
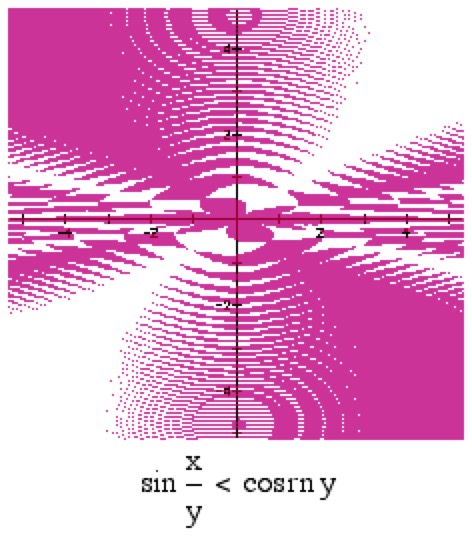
Mathematics and Art
Comprehensive article exploring the close relationship between math and art throughout the centuries.
Seven Times Mathematics Became Art and Blew Our Minds
Science Alert article highlights seven modern instances in which math and art imitate each other in beautiful ways.
Using Ancient Mathematics to Enrich Your Design Skills
Nowhere is the magical intersection of art and mathematics more clear than in areas comprising the broad field of design.
Making Mathematical Art
"Stunning symmetrical images created with just a few equations and a computer." From the venerable Scientific American.
Why the History of Maths is Also the History of Art
Article in The Guardian exploring how artists have utilized the inherent beauty of mathematical ideas in their work for thousands of years (at least).
Fifty Famous Curves
The title says it all. 50 fascinating general mathematical curves: Sinusoidal Spirals, Nephroids and Lissajous Curves, Fermat's Spiral, Epitrochoid/Epicycloid, more.
List of Curves
Wikipedia's accessible yet comprehensive index of articles discussing mathematical curves, their forms, properties.
Wolfram Alpha Examples: Popular Curves
Yes, you can actually use mathematical relations to draw interesting, creative portraits of luminaries like Lady Gaga and Mew.
GeoGebra: Math in Art
A gallery of beautiful but simple GeoGebra math art projects. Sliders enable interactivity, learning by exploration. A playground for budding math artists.
Orbiform
None other than Leonhard Euler proved the constant width of this intriguing solid. Acts like a sphere, looks like a ... what? Artsy artillery shell? Details here.
Check out my Math-as-Art blog featuring additional original 2D and 3D graphs like those shown above.
There's no better way to refute the notion of the lifeless sterility of mathematics than to visit the Wolfram Demonstrations Project. I urge you to take a moment to enjoy the delightful mathematical objects you'll find there.
Unfortunately, many students have been mistaught that math is a dry, rote, one-dimensional activity devoid of originality or inventiveness and lacking any real connection to the arts.
Fortunately for me, I was not one of them.
On the contrary, I've always been enthralled by the astonishing musicality of mathematics and entranced by its subtle aesthetics, alluring forms, and fascinating puzzles to be solved.
Advances in computing technology have made possible the widespread discovery and appreciation of the sublime beauty of mathematics. The art of math can now be enjoyed by all!
I hope you'll delight in the following graphs of mathematical relations I created involving nothing more sophisticated than high school precalculus.
Pretty Precalculus Graphs
Designed in 2018 using Google Search's graphing calculator:

Egg Carton
z = sin(x/2)+cos(y/2)

Wrinkled Paper
z = x-y+tan(x)-cos(8x-sin(2y))

Fancy Lapels
z = arcsec(sin(1/x)-cos(1/y))

Corrugated V-Roof
z = abs(sin(2x)-y)

Bed o' Nails
z = sin(4y)+cos(4x)

Arizona Desert
z = (x-y)/(sin(x)+1/cos(y))

Celery Row
z = (sin(x)cos(y))/(x-y)

Three Fingers
z = log(sin(1.1x)-y)

Plastic Chair
z = -abs(x)+2x^4-abs(x^2*y^3)

Lettuce Garden
z = 1/(sin(x)-cos(y))
Designed in 2018 using Wolfram Alpha:

Dimpled Vase
z^2 = x^6-x^2+y^6+y^2


Mesa Group with Hills and Valleys
z = sin(2x)cos(2y)exp(-(x^2+y^2)/6)


Slanting Waves
z = xsin(y)


Tartan Forest
z = tan(.01sin(x)cos(y))^2


Techtonic Rift
z = x^3+tan(y)+cot(x)+y^3

Squarish Tube
x^2-y^3+z^4 = 1


Spikes
z = tan(sin(x)cos(y))^2


Wavy Incline
z = -cos(xy)+y


Gaping Maw
z = (x^2+1.5y^2)*e^(-x^2-y^2)


X Marks the Spot
z = (arccos(abs(x)+abs(y))/arcsin(abs(x)-abs(y))
Designed in 2018 using Apple's Grapher app:

Splotches
sin(sin(x)+cos(y)) = cos(sin(xy)+cos(x))

Slinky Toy
x = sin(t^2)
y = cos(t)
t = {0..10}

The Wiggles
cos(2x)-sin(xy)-tan(2y) = .5

Basket Math
x = cos(11t)
y = sin(13t)
t = {0..2π}

Double-Back
r = t^2-t
𝜃 = tsin(t)
t = {0..40}

Line Dancing
cos(x^2)+sin(xy)+tan(y^2) = 1

Controlled Chaos
x^3 = 1+7tan(xy^2)

Ripples
sin(xy) = cos(y)+sin(x)

Convergence
y = kx/3
k = {1..18}

Spiral
x = (u/5)cos(u)
y = (u/5)sin(u)
u = {0..20}

Fender Butterfly
r = sec(x)
y = tan(x)+cot(x)+K
k = {-5..5}
Designed in the late 1990's using the pioneering Mac app Graphing Calculator, later NuCalc:










Articles
Mathematics and Art
Comprehensive article exploring the close relationship between math and art throughout the centuries.
Seven Times Mathematics Became Art and Blew Our Minds
Science Alert article highlights seven modern instances in which math and art imitate each other in beautiful ways.
Using Ancient Mathematics to Enrich Your Design Skills
Nowhere is the magical intersection of art and mathematics more clear than in areas comprising the broad field of design.
Making Mathematical Art
"Stunning symmetrical images created with just a few equations and a computer." From the venerable Scientific American.
Why the History of Maths is Also the History of Art
Article in The Guardian exploring how artists have utilized the inherent beauty of mathematical ideas in their work for thousands of years (at least).
Fifty Famous Curves
The title says it all. 50 fascinating general mathematical curves: Sinusoidal Spirals, Nephroids and Lissajous Curves, Fermat's Spiral, Epitrochoid/Epicycloid, more.
List of Curves
Wikipedia's accessible yet comprehensive index of articles discussing mathematical curves, their forms, properties.
Wolfram Alpha Examples: Popular Curves
Yes, you can actually use mathematical relations to draw interesting, creative portraits of luminaries like Lady Gaga and Mew.
Other
GeoGebra: Math in Art
A gallery of beautiful but simple GeoGebra math art projects. Sliders enable interactivity, learning by exploration. A playground for budding math artists.
Orbiform
None other than Leonhard Euler proved the constant width of this intriguing solid. Acts like a sphere, looks like a ... what? Artsy artillery shell? Details here.
More!
Check out my Math-as-Art blog featuring additional original 2D and 3D graphs like those shown above.
There's no better way to refute the notion of the lifeless sterility of mathematics than to visit the Wolfram Demonstrations Project. I urge you to take a moment to enjoy the delightful mathematical objects you'll find there.
- > Home
- > Services
- > Math as Art